High-Performance R-Theta Stage Motion Systems for Semiconductor Tools
2-Axis Motion Systems based on Polar Coordinates vs. conventional XY Stages
From the ocean-view decks of the Monterey Bay Aquarium, at a distance from the rocky shoreline outcrop, the fingerprint-like patterns of Humpback Whale tail flukes suddenly appear. To an observer on the deck, a hurried and excited description would soon follow. It’s this simple description that masks much deeper concepts that trace historical roots to Newton, symmetry arguments, and today can be found in cutting edge semiconductor process tools.
From Descartes to Newton
Any description to a fellow human on where to find the whale would likely use information based on the polar coordinate system. Something like “at your 3 o’clock, about 500 feet out” would be a simple and effective instruction. It’s the curious commonality of description among observers that reveals a meaningful deeper non-intuitive truth. The whale is some radial distance off the coast (relative to observer) at some angle referenced against direct line of sight. It’s clear the description isn’t based on the more common Cartesian coordinate system (using X and Y to locate the whale) but on a polar coordinate system using R (radial distance from a pole) and Theta (rotation angle relative to reference). The polar coordinate system, as it would come to be known, was first applied in such a way by Isaac Newton in the late 17th century.
Polar coordinates, in this case, are the more intuitive system to work in and can be especially useful to simplify math operations on radially symmetric functions and spiral motion path programming. This extension of coordinate system convention into practical precision automation system configuration has very specific performance and programmatic implications. It’s the more nuanced implications of engineering such systems that can inform the more optimal approach.
Compactness: King of Clean Rooms and Dynamics

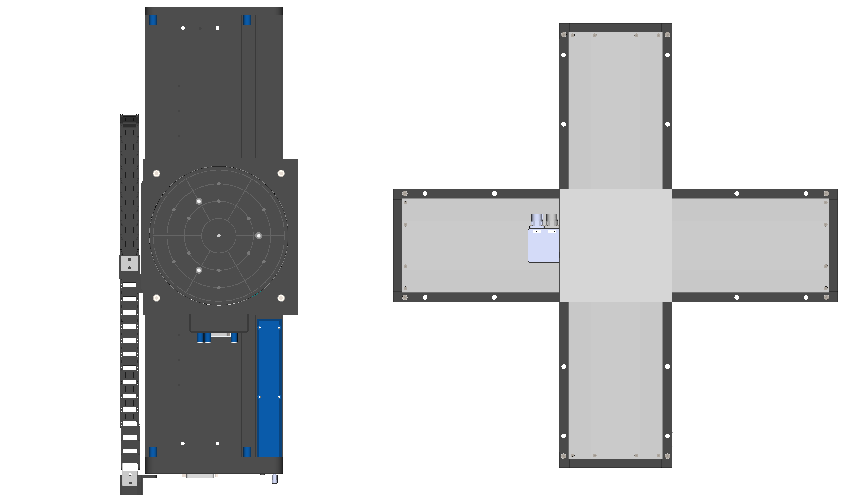
In many applications, especially with systems deployed in clean rooms, compactness is an important consideration for systems configuration. Compactness of motion and positioning systems also plays especially into dynamic performance and parasitic motion type runout errors. Comparatively, the compactness of similarly configured high performance R-Theta and XY Stage Systems demonstrates the space savings typical to an R-Theta based tool. Here the lower axis would be quite similarly scaled, but the orthogonal Y-Axis replaced by a rotation stage has considerably smaller footprint.
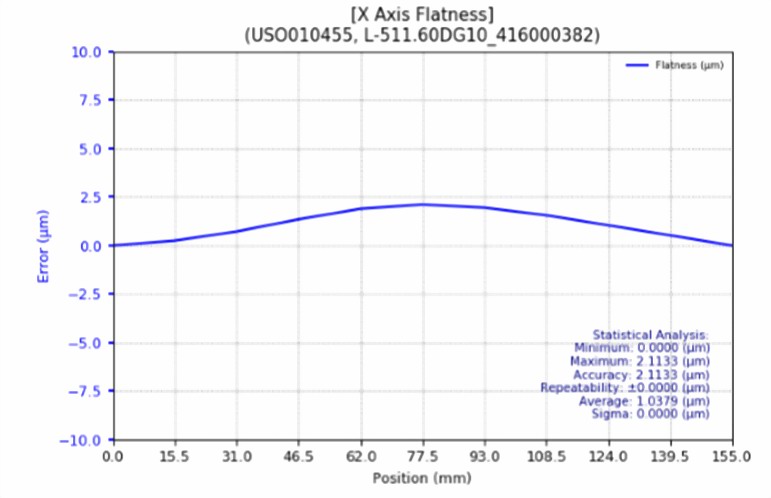
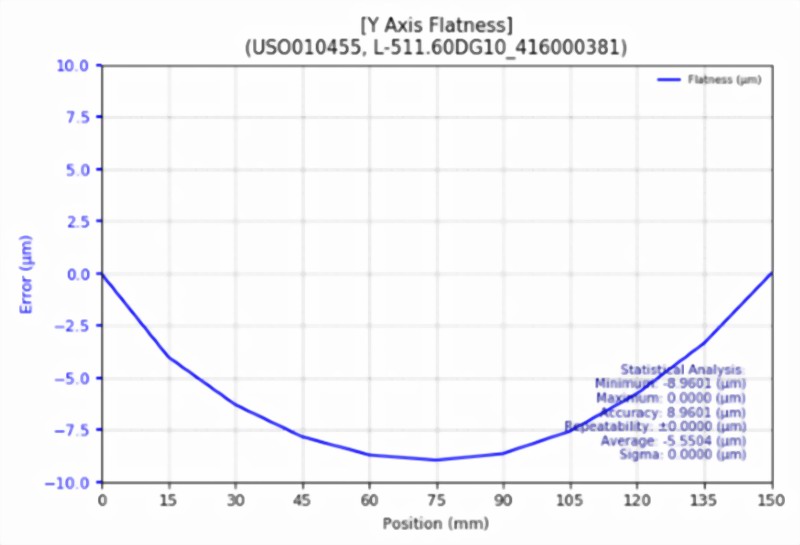
This compactness also comes with a typical net weight reduction in terms of applied load on the lower stage axis. The smaller load improves top-end stage dynamics, while reducing motor heating and inertia related performance limitations and extending mechanical bearing lifetimes. This configuration also reduces cantilevered loading and the pitch and flatness errors that go along with it and – needless to mention the positive effect on improving bearing / stage lifetime.
X and Y flatness measurements on an XYZ linear stage shows the effect of the cantilevered, loaded Y axis on flatness.
High RPMs: Continuous Rotation beats Stop and Go
The upper axis dynamics also optimize throughput especially on curvilinear arc type motion paths. This motion type can be achieved with pure rotation or through synchronized XY motion. A comparison of the relative dynamics demonstrates the advantages of the R-Theta configuration. Consider a rotational rotation speed of 1440°/second (or 480 RPM) with a 200mm radius of curvature. This motion translates to an XY motion with an average velocity of ~4.8 m/s. In the XY stage system, that arc path requires each linear translation stage to accelerate and decelerate as motion transitions from pure X to pure Y-axis motion. This continuous acceleration / deceleration is very demanding, especially in a stacked stage configuration where inertia on the lower stage axis requires high-acceleration and jerk to maintain high-throughput with implications to precision performance (in this case following error), angular runout errors (pitching on acceleration), and motor heating limitations. PI offers a highly effective control algorithms to reduce motor loads optimize dynamic performance (PILOT).
High Precision Flying
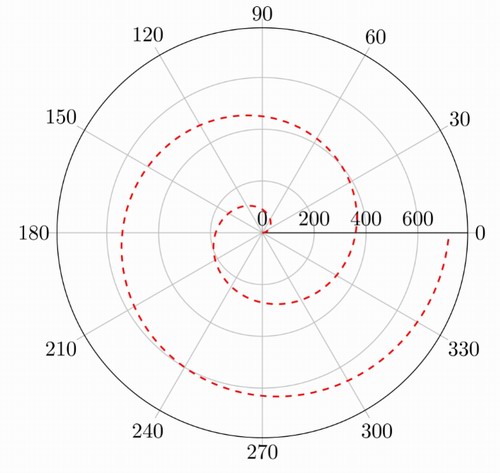
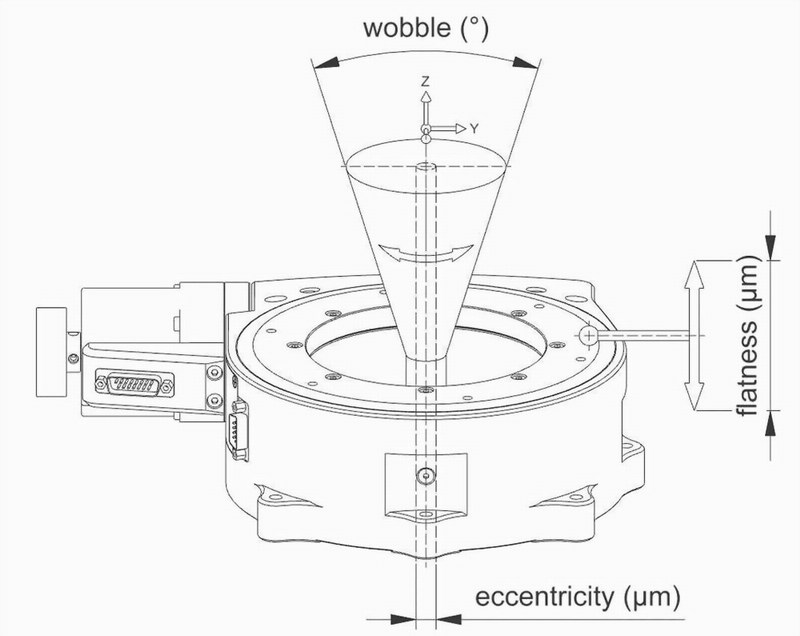
Looking comparatively at runout error, one potential drawback to an R-θ configuration is Abbe error amplified linear runout associated with rotation stage wobble.
Wobble is tilting of the rotation axis relative to an ideal vector (normal to the rotation plane). This can have a dramatic impact in terms of precision performance characteristics (especially at larger distance from axis of rotation). Taking the case described above (with points of interest, 200 mm away), even a minimal ± 50 µrad error can result in ±10 µm of runout error.
To minimize this type of runout error, air bearing rotary tables can be used. Air bearings offer improved guiding performances over mechanical bearing counterparts (essentially floating over precision reference surfaces). As one example, a PI A-634 Air Bearing Rotation Stage can achieve wobble performance of only ±1µrad, resulting in ±0.2µm of runout error (again at 200mm distance). High precision air bearing rotation stages are also clean, non-wearing, and maintenance free - which is especially important for high duty cycle operations with continuous spin operation.
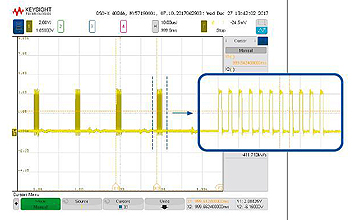
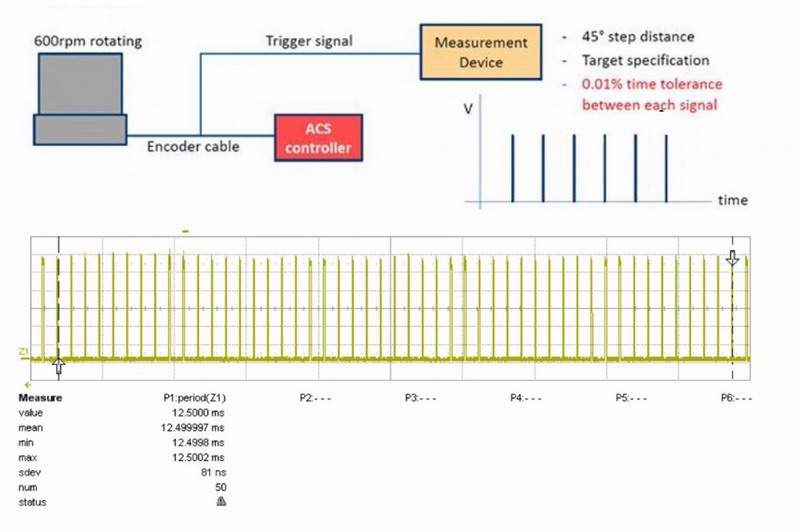
Ultrafast Triggers to Synchronize Motion with Cameras, Lasers, and Metrology Equipment
In many inspection and metrology processes, a motion synchronized fast trigger signal is required. Historically, high-speed triggers required digital encoder signals. In the recent past, this constraint has been removed and very accurate high-speed motion synchronized triggering can be done with absolute encoders or analog (sin/cos encoder) signals – thereby, opening up a new avenue to higher precision, and safer, and simplified solutions. In this case with R-Theta configured systems, a multi-axis trigger would work congruently as an XY position trigger, with the coordinate specifications simply defined in polar coordinates.
Application Optimized Engineered Motion Systems
PI offers a broad catalog of rotary, R-Theta, and Linear Stages and application-specific engineered systems including granite motion systems, based on air bearing and mechanical bearing designs. A couple of examples ranging from highest performance focus to economical affordability are presented below:



Please do not hesitate to contact our application engineers with any questions you have regarding your next precision positioning and motion control project.

Blog Categories
- Aero-Space
- Air Bearing Stages, Components, Systems
- Astronomy
- Automation, Nano-Automation
- Beamline Instrumentation
- Bio-Medical
- Hexapods
- Imaging & Microscopy
- Laser Machining, Processing
- Linear Actuators
- Linear Motor, Positioning System
- Metrology
- Microscopy
- Motorized Precision Positioners
- Multi-Axis Motion
- Nanopositioning
- Photonics
- Piezo Actuators, Motors
- Piezo Mechanics
- Piezo Transducers / Sensors
- Precision Machining
- Semicon
- Software Tools
- UHV Positioning Stage
- Voice Coil Linear Actuator
- X-Ray Spectroscopy