Basic Designs of Piezoelectric Positioning Elements: Piezo Stacks and Tubes
Stack Design
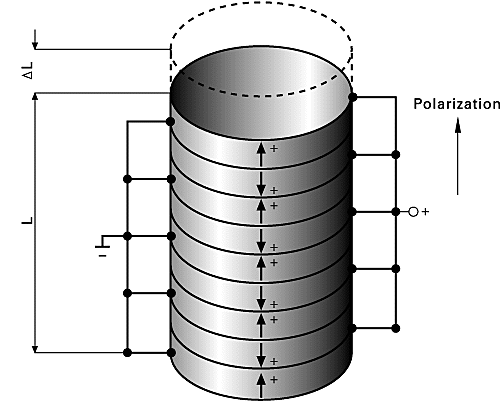
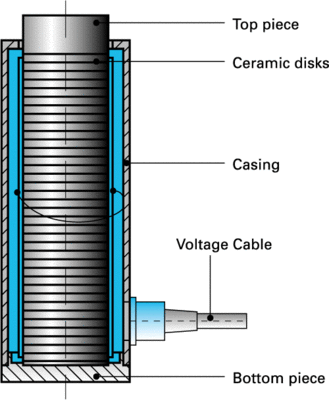
The active part of the positioning element consists of a stack of ceramic disks separated by thin metallic electrodes. Maximum operating voltage is proportional to the thickness of the disks. PI stack actuators are manufactured with layers from 0.02 to 1 mm thickness.
Stack elements can withstand high pressure and show the highest stiffness of all piezo actuator designs. Since the ceramics cannot withstand large pulling forces, spring preloaded actuators are available. Stack models can be used for static and dynamic operation.
Displacement of a Piezo stack actuator can be estimated by the following equation:
DL » d33*n * U (4-24)
where
d33 = strain coefficient (field and deflection in polarization direction) [m/V]
n = number of ceramic layers
U = operating voltage [V]
Example:
P-845
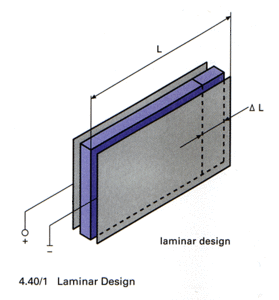
Laminar Design / Tube Design (Contraction Type Actuator)
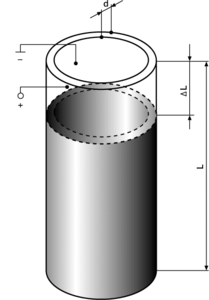
The active material in the laminar actuators consists of thin ceramic strips, or tubes. The displacement of these actuators is perpendicular to the direction of polarization and electric field. When the volt-age is increased the strip contracts. The piezo strain coefficient d31 (negative!) describes the relative change in length. It is on the order of 50% of d33.
The maximum travel is a function of the length of the strips, while the number of strips arranged in parallel determines the stiffness and the stability of the element.
Displacement of a Piezo contraction actuator can be estimated by the following equation:
ΔL ≈ d31*L * U/d (4-25)
where
d31 = strain coefficient (deflection normal to polarization direction) [m/V]
L = length of the Piezo ceramics [m]
U = operating voltage [V]
d = thickness of one ceramic layer [m]
Example:
Laminar piezos are used in the P-280. P-282 Flexure Positioners
Pieze Tube Scanner Examples:
PT-120 to PT-140 Piezo Tubes
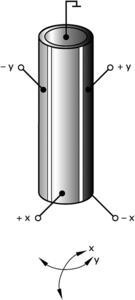
Monolithic ceramic tubes are yet another form of piezo actuator. Tubes are silvered inside and out and operate on the transversal piezo effect. When an electric voltage is applied between the outer and inner diameter, the tube contracts axially and radially. Axial contraction can be estimated by the following equation:
ΔL ≈ d31*L * U/d (4-26a)
where
d31 = strain coefficient (deflection normal to polarization direction) [m/V]
L = length of the Piezo ceramic tube [m]
U = operating voltage [V]
d = wall thickness [m]
Δd ≈ d33 * U (4-26b)
where
Δd = change in wall thickness [m]
d33 = strain coefficient (field and deflection in polarization direction) [m/V]
U = operating voltage [V]
The radial contraction is a superposition of several effects and cannot be ex-pressed by a simple equation.
When the outside electrode of a tube is separated into four 90° segments, differential drive voltage of opposing electrodes will lead to bending of one end (if the other end is clamped). Scanner tubes that flex in X and Y are widely used in scanning probe microscopes.
The scan range of a scanner tube is defined by
Δx » (2√2 * d31 * U * L2) / (π * ID * d) (4-27)
Where
Δx = scan range in X and Y (for symmetrical electrodes) [m]
d31 = strain coefficient (deflection normal to polarization direction) [m/V]
U = operating voltage [V]
L = length [m]
ID = inner diameter [m]
d = wall thickness [m]
Tube actuators are not designed to withstand large forces. Application examples are scanning microscopy, ink jet printers etc.
If you have any questions, ask a PI engineer for help.